Published on

How Machine Learning Models Work

Authors
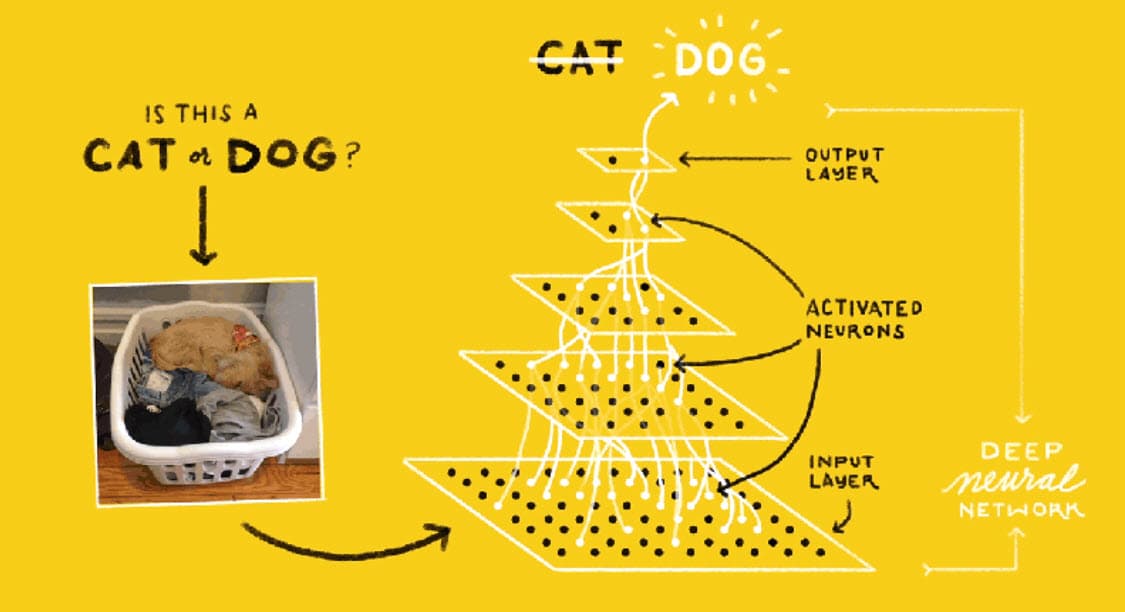
How the brain works versus how machine learning models work

Machine learning is a subset of artificial intelligence (AI) that focuses on developing algorithms that allow computers to learn from and make predictions or decisions based on data.1 These algorithms are designed to identify patterns in data and use them to make informed decisions without being explicitly programmed to do so.2 In essence, machine learning models are trained to recognize patterns and make predictions based on new data.3

Important Terms

Before diving into how machine learning models work, let's define some key terms:

  • Artificial Neural Network: Artificial neural networks are loosely based on how we believe the brain is structured. Just as the brain looks at an object or an animal’s features and then predicts what that object or animal is, an ML model is trained on features and calculates the probabilities for its predictions using mathematics instead of biology. When these artificial neurons are connected in multiple layers, they are called deep neural networks.4
  • Artificial Neurons & Perceptrons: The artificial neuron is the basic unit or element of a neural network. One type of artificial neuron is the perceptron. The perceptron is the basic building block of ML that takes in input data and transforms inputs into some output number if it crosses some threshold for activation.5

Biological Inspiration

Drawing an analogy to artificial intelligence, machine learning employs artificial neural networks that loosely mimic the human brain's structure and functionality. These networks, particularly in their deep learning iterations, utilize multiple layers of interconnected neurons to recognize and interpret complex patterns and features within data.6

The Basic Operation of a Perceptron

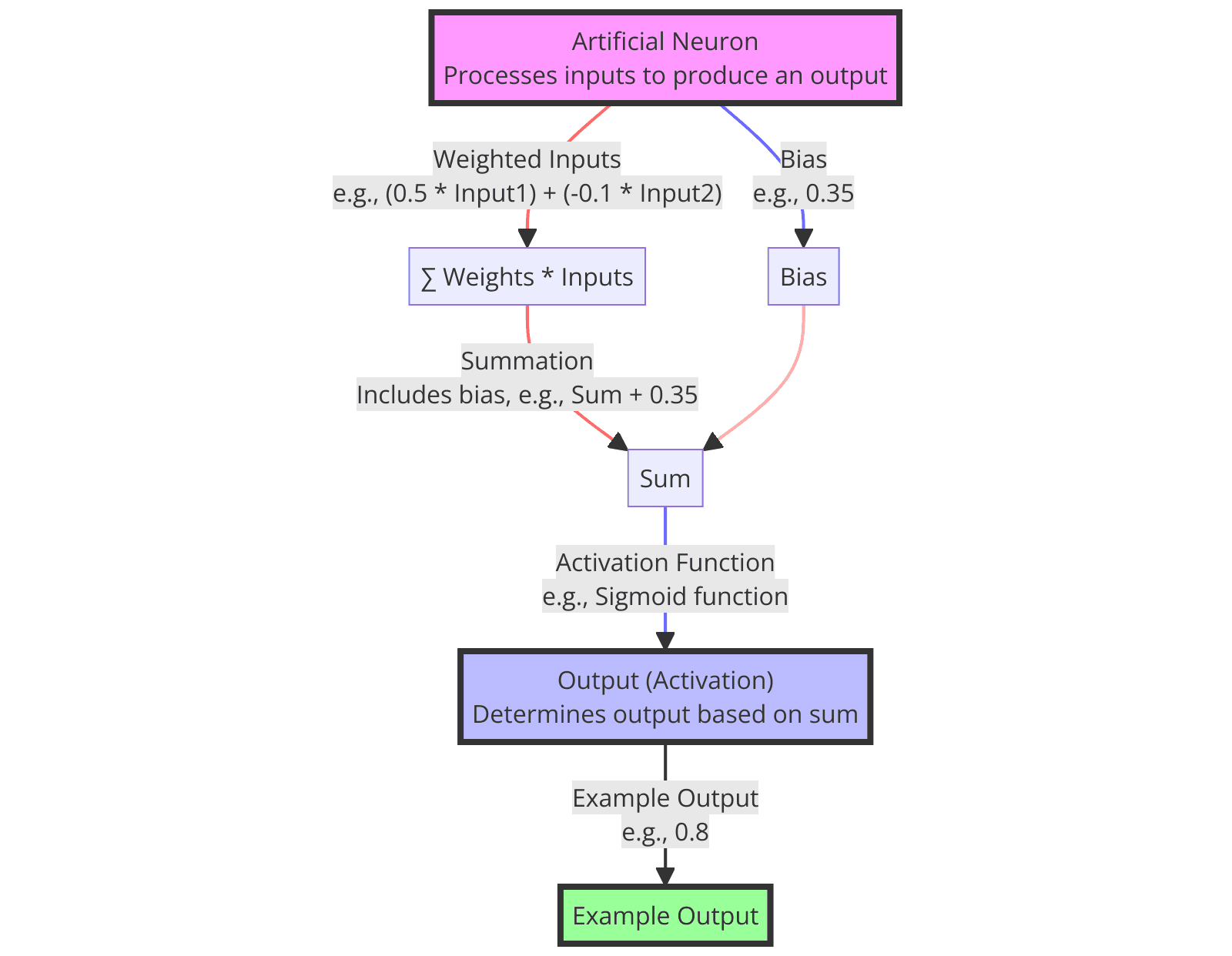
Perceptrons are the fundamental building blocks of artificial neural networks, serving as the basic unit that processes input data and produces an output.7 The operation of a perceptron involves multiplying each input by its corresponding weight, summing these products together, and then adding the bias.8 This process results in a total that, through the application of an activation function, determines whether the perceptron activates, emitting a binary output based on whether the total exceeds a certain threshold.9

Inputs of a Perceptron

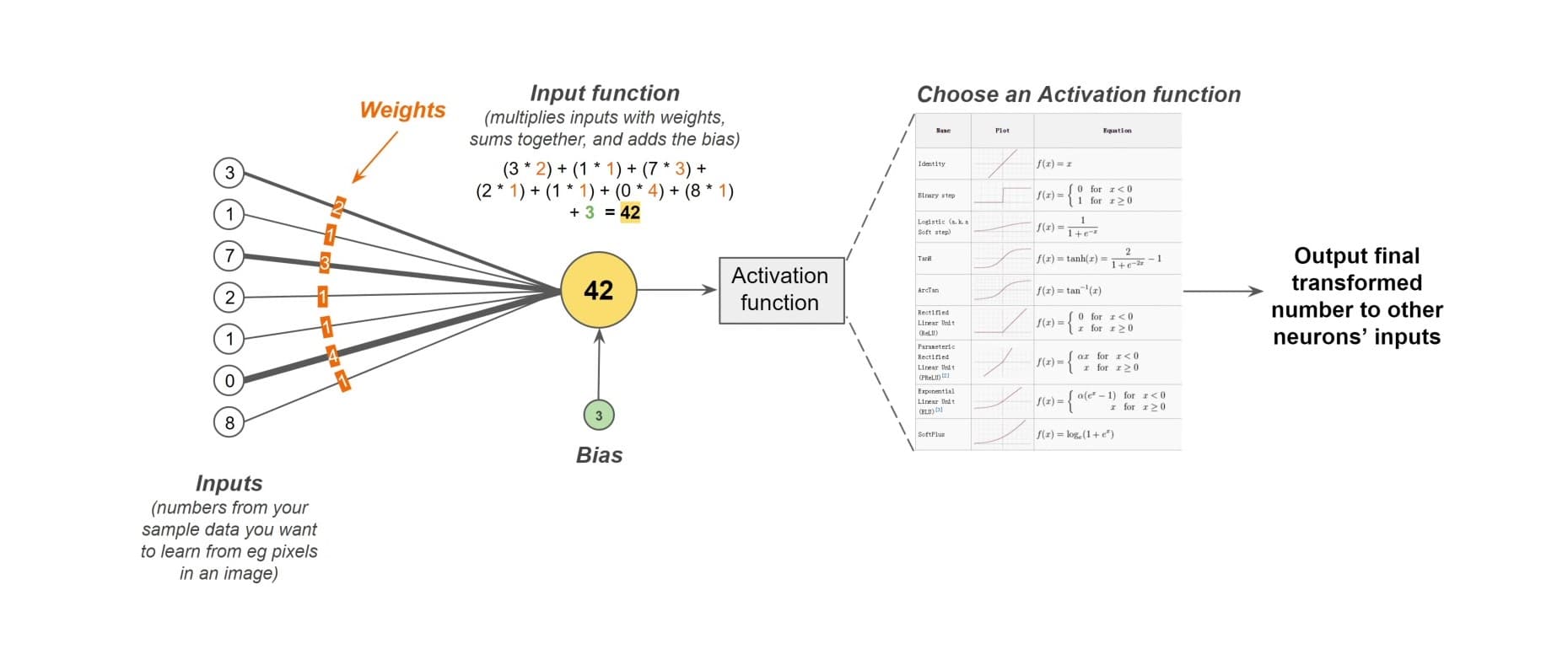
Zooming in on the individual components of these networks reveals the perceptron, a type of artificial neuron that dates back to the 1950s and serves as a fundamental building block in machine learning.10 The perceptron operates by sampling numerical inputs—each representing a specific feature from the data it's analyzing.11 These inputs are typically normalized between 0 and 1 to ensure relative comparability, although for illustrative purposes, whole numbers are often used in explanations.12

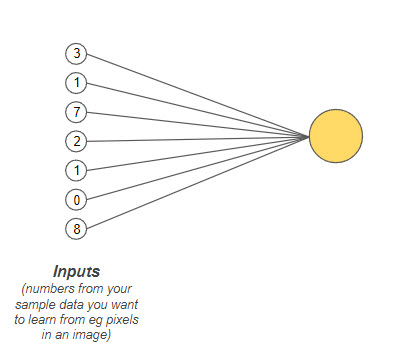
Single perceptron with multiple inputs. Figure 4.3.1.2. Single Perceptron with Multiple Inputs, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

For example, the above diagram shows a single perceptron receiving multiple numerical inputs. These numbers are the sample data from which you want your model to learn. Each input represents a feature for an item in your data. This example has seven input values, but if you use a 100x100 grayscale image, there will be 10,000 input values as each pixel would be a feature! A single neuron can have as many inputs as needed to sample all the input data.

Weights & Bias of a Perceptron

A perceptron's inputs are each assigned a weight, indicating the importance of that input in the overall calculation.13 Initially, these weights are set to random values, establishing a baseline from which the learning process begins.14 Alongside weights, a bias—a randomly chosen number—is added to the equation to enable the perceptron to adjust its output threshold during the learning phase.15

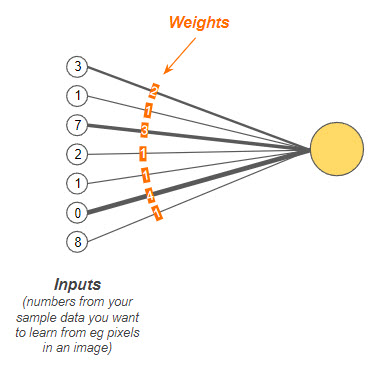
Single perceptron with multiple inputs and weights Figure 4.3.1.3. Single Perceptron with Multiple Inputs and Weights, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

The visualization above shows the “weight” given to each of the input signals. Observe that the thicker lines carry greater weight than the thinner ones in this diagram. Heavier weights contribute more to the value that is calculated in the perceptron. The weights allow the neuron to amplify or suppress the value of each input based on the importance of the input.16 Before the perceptron is trained, the weights are randomly chosen to start with. So outputs will also seem pretty random at first before training.17

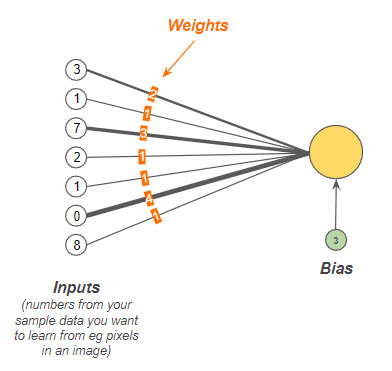
Single perceptron with multiple inputs, Weights and Biases Figure 4.3.1.4 Single Perceptron with Multiple Inputs, Weights and Biases Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

To compare, the above diagram shows a new parameter called the ‘bias’ added to the model. In this case, the ‘bias’ is randomly chosen to be 3. It is also randomly initialized at the start. The bias can be changed during the learning process if needed.18

The Calculation Process of a Perceptron

The operation of a perceptron involves multiplying each input by its corresponding weight, summing these products together, and then adding the bias.19 This process results in a total that, through the application of an activation function, determines whether the perceptron activates, emitting a binary output based on whether the total exceeds a certain threshold.20

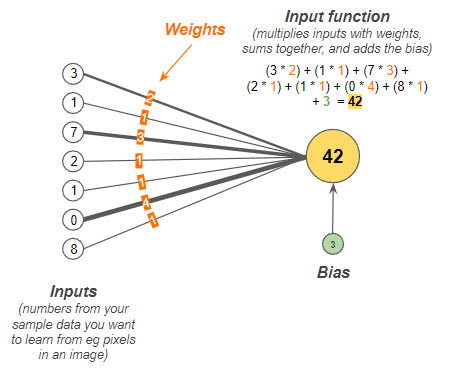
Single perceptron input function. Figure 4.3.1.5. Single Perceptron Input Function, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

The diagram of the single perceptron input function above shows how the first half of the perceptron works. Each input value is multiplied by its corresponding weight. The resulting products of all the input values and their weights are summed together. The bias value is added to the sum obtained in the previous step. The final value (42) is shown in the perceptron in the yellow circle, if you were to calculate the multiplications of inputs, sum them, and then add the bias.

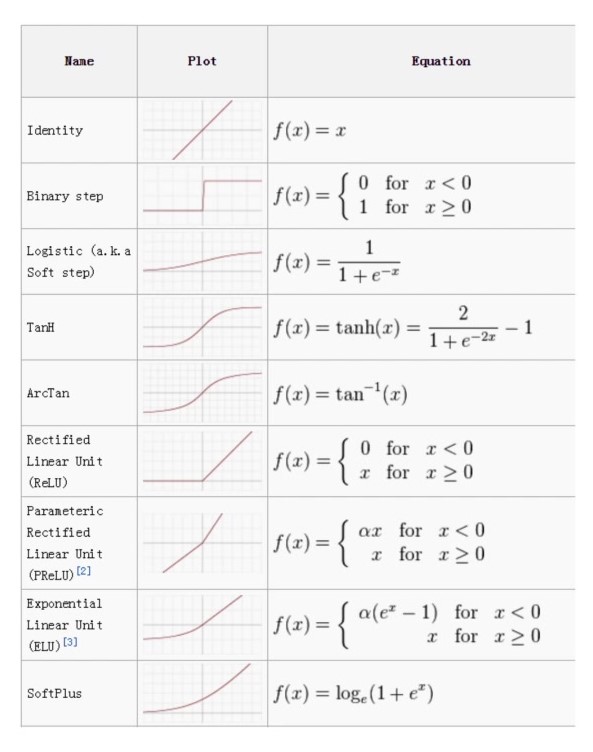
Activation Functions

Activation functions are essential in this context, transforming the weighted sum into an output that dictates the neuron's activation.21 These functions vary, with some allowing for straightforward pass-through of the input value and others, like the Rectified Linear Unit (ReLU), introducing non-linearities beneficial for certain tasks.22 Activation functions define when a neuron activates to produce an output.23

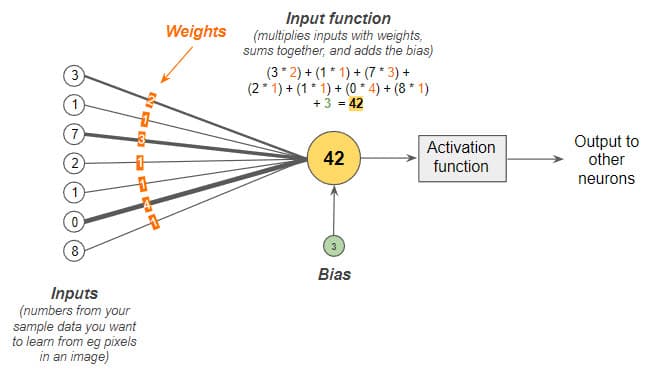
Single Perceptron Activation Function Figure 4.3.1.6. Single Perceptron Activation Function, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

The image above shows how the activation function works, which is the final part of the perceptron. Put simply, the activation function activates the neuron to provide an output number if the total calculated is greater than a threshold.

To illustrate things further, consider the graph below:

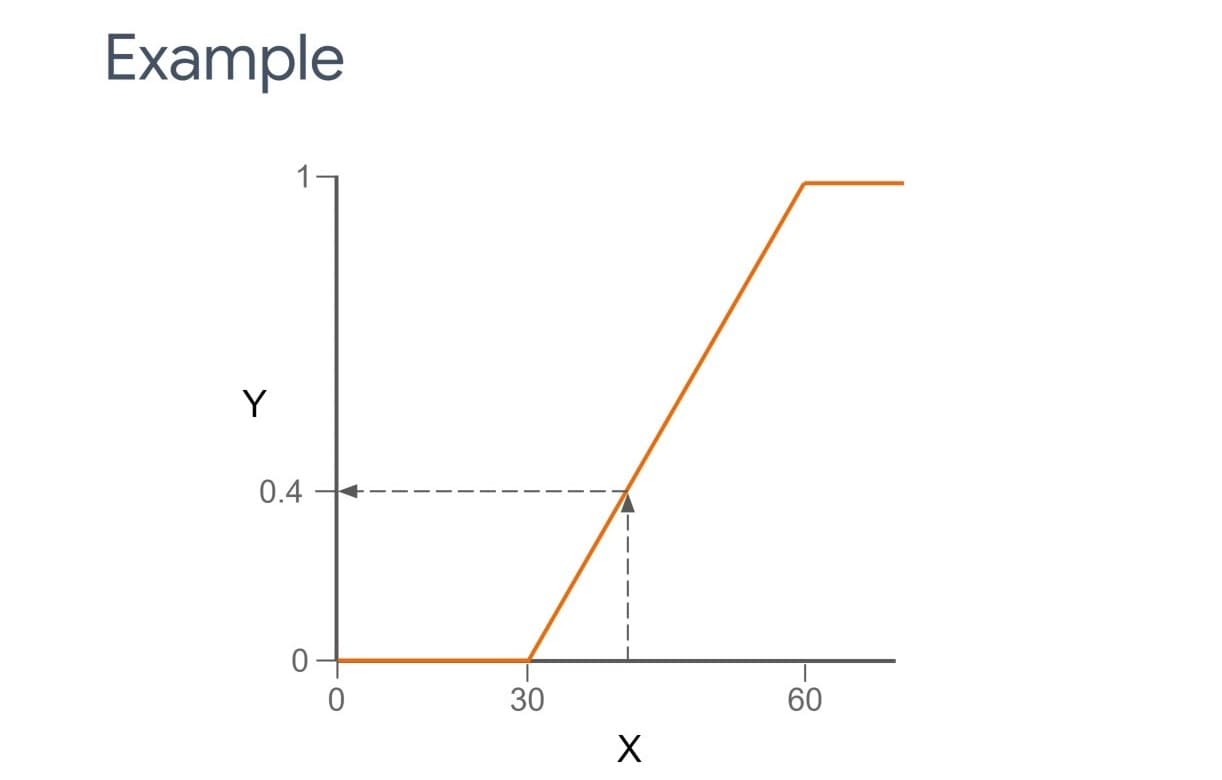
Example activation function. Figure 4.3.1.7, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

For all values of ‘x’ that are less than 30, the ‘y’ output is 0. For ‘x’ values that increase from 30 to 60, the ‘y’ output steadily increases between 0 and 1. For all ‘x’ values above 60, the ‘y’ output remains at 1. If your ‘x’ value were to be 42, the ‘y’ output would be roughly 0.4 in this graph. The neuron will now activate based on the threshold you have decided for the model with 0.4 as an output of the neuron.

For example, ReLU is an example of a popular activation function. The function returns 0 if ‘x’ is less than 0, but returns x in all other cases with no upper limit, it just passes through numbers that are above 0. ReLU is an example of a non-linear activation function as it is not a single straight line like the identity function shown above.24

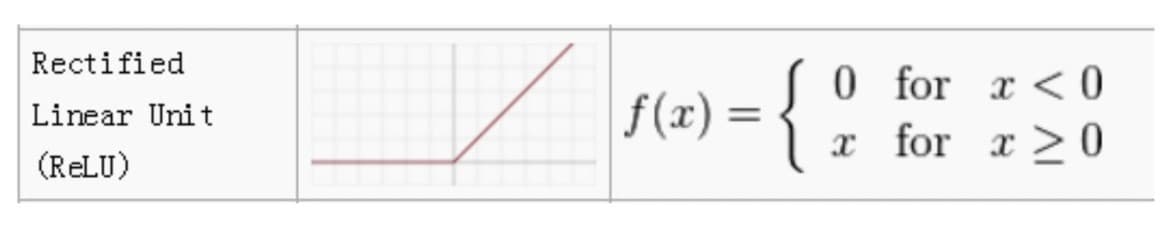
ReLU activation function example. Figure 4.3.1.9. The ReLU Activation Function, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

There is a range of distinct activation functions available, some suited to particular tasks.25 The chart below shows some more common ones:

A list of common activation functions. Figure 4.3.1.8. Activation Functions, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

Putting it all together: The Role of the Perceptron in Machine Learning

First, inputs are multiplied by their corresponding weights, the totals are added, and a bias is added to arrive at a grand total.26 Next, the grand total is sent through an activation function that transforms the number into an output value.27 The activation function outputs either a 1 or a 0 based on some defined threshold. A perceptron, in short, turns inputs into binary outputs.28

A complete diagram of a perceptron's process. Figure 4.3.1.10. Complete Perceptron Diagram, Jason Mayes, Google WebML 102, Google AI for JavaScript developers with Tensor Flow.js, Chapter 4: Writing Custom Models, Lesson 3.1: Perceptrons and Neurons

The perceptron's binary output—either a 0 or a 1—makes it distinct from other types of neurons that might produce a range of values29. This binary decision-making capability encapsulates the perceptron's fundamental role in machine learning, offering a simple yet powerful tool for classification tasks30.

Diagram showing the binary output of a perceptron.

In essence, the perceptron exemplifies the convergence of biological inspiration and mathematical precision, embodying a foundational concept in machine learning31. Through the perceptron, we gain not only insight into the computational imitation of human cognition but also a versatile tool for navigating the ever-expanding landscape of artificial intelligence32.

Footnotes

  1. Yann LeCun, Yoshua Bengio & Geoffrey Hinton, Deep Learning, 521 Nature 436, 436-444 (2015). ↩

  2. Aidong Zhang & Xiaoli Zhang Fern, Recent Advances in Transfer Learning for Cross-Domain Data Fusion, 62 Info. Fusion 19, 19-22 (2020). ↩

  3. Jürgen Schmidhuber, Deep Learning in Neural Networks: An Overview, 61 Neural Networks 85, 85-117 (2015). ↩

  4. Alex Krizhevsky, Ilya Sutskever & Geoffrey Hinton, ImageNet Classification with Deep Convolutional Neural Networks, 60 Commun. ACM 84, 84-90 (2017). ↩

  5. Jürgen Schmidhuber, Deep Learning in Neural Networks: An Overview, 61 Neural Networks 85, 85-117 (2015); Yoshua Bengio, Ian Goodfellow & Aaron Courville, Deep Learning, 19 MIT Press 45, 45-56 (2016). ↩

  6. Mohammad Mustafa Taye, Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions, 12 Computers 91, 91-106 (2023); Alex Krizhevsky, Ilya Sutskever & Geoffrey Hinton, ImageNet Classification with Deep Convolutional Neural Networks, 60 Commun. ACM 84, 84-90 (2017); Yann LeCun, Yoshua Bengio & Geoffrey Hinton, Deep Learning, 521 Nature 436, 436-444 (2015). ↩

  7. Frank Rosenblatt, The Perceptron - A Perceiving and Recognizing Automation, Report 85-460, Cornell Aeronautical Laboratory, 1957. ↩

  8. Navin Kumar Manaswi, Multilayer Perceptron, in Deep Learning with Applications Using Python, Berkeley, CA, 2018. ↩

  9. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  10. Ke-Lin Du et al., Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era, 10 Mathematics 4730, 4730-4748 (2022). ↩

  11. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  12. M. Mustafa Taye, Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions, 12 Computers 91, 91-106 (2023). ↩

  13. Navin Kumar Manaswi, Multilayer Perceptron, in Deep Learning with Applications Using Python, Berkeley, CA, 2018. ↩

  14. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  15. Ke-Lin Du et al., Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era, 10 Mathematics 4730, 4730-4748 (2022). ↩

  16. Frank Rosenblatt, The Perceptron - A Perceiving and Recognizing Automation, Report 85-460, Cornell Aeronautical Laboratory, 1957. ↩

  17. S. Haykin, Neural Networks: A Comprehensive Foundation, Prentice Hall PTR, 1998. ↩

  18. S. Haykin, Neural Networks: A Comprehensive Foundation, Prentice Hall PTR, 1998. ↩

  19. Klaus D. Toennies, 7 Multi-Layer Perceptron for Image Classification, in An Introduction to Image Classification, Singapore, 2024. ↩

  20. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  21. LeCun, Y., et al., Efficient backpropagation, in Neural Networks: Tricks of the Trade, Berlin, 1998. ↩

  22. Ramachandran, P., Zoph, B., & Le, Q.V., Searching for activation functions, Proceedings of the IEEE International Conference on Computer Vision, 2018. ↩

  23. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  24. Nair, V., & Hinton, G.E., Rectified linear units improve restricted boltzmann machines, Proceedings of the 27th International Conference on International Conference on Machine Learning, 2010. ↩

  25. S. Haykin, Neural Networks: A Comprehensive Foundation, Prentice Hall PTR, 1998. ↩

  26. Navin Kumar Manaswi, Multilayer Perceptron, in Deep Learning with Applications Using Python, Berkeley, CA, 2018. ↩

  27. LeCun, Y., et al., Efficient Backpropagation in Neural Networks: Tricks of the Trade, Berlin, 1998. ↩

  28. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  29. Ramachandran, P., Zoph, B., & Le, Q.V., Searching for activation functions, Proceedings of the IEEE International Conference on Computer Vision, 2018. ↩

  30. Klaus D. Toennies, 7 Multi-Layer Perceptron for Image Classification, in An Introduction to Image Classification, Singapore, 2024. ↩

  31. Ameet V. Joshi, Perceptron and Neural Networks, in Machine Learning and Artificial Intelligence, Cham, 2023. ↩

  32. S. Haykin, Neural Networks: A Comprehensive Foundation, Prentice Hall PTR, 1998. ↩

Discuss on Twitter • View on GitHub